Is your Facebook ROI £2.50? Or is it somewhere between £2- £3?

The value of measuring uncertainty

In the world of Marketing Mix Modelling (MMM), it's easy to become fixated on point estimates.

• What’s the ROI of this channel?
• What’s the expected uplift from that spend?

MMM uses a statistical modelling approach. Traditional regression models (often called frequentist) give us just that: a single number. But what if that number is only part of the story?

Bayesian approaches to MMM introduce something deeper: uncertainty. Instead of producing a single “best guess,” Bayesian models produce distributions.

At first glance, this may seem like a technical nuance. In reality, it opens the door to better decision-making, especially in areas like ROI interpretation, budget optimisation, and risk management.

Point ROI vs. ROI Distributions

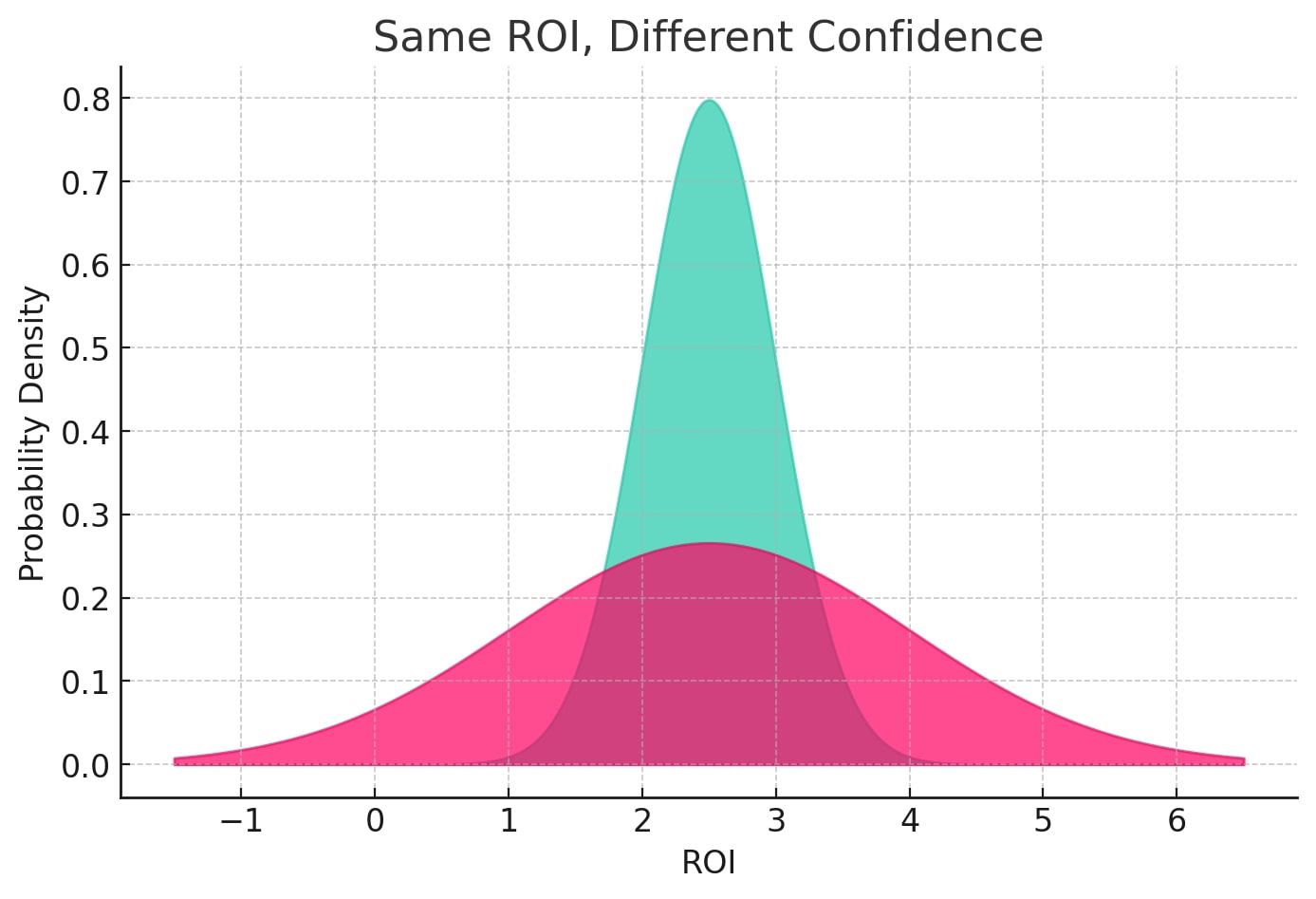
Imagine two media channels: Channel A and Channel B. Each showing an average ROI of £/€2.5. If you were working only with point estimates, you might treat them as equally viable. But Bayesian modelling allows us to dive deeper into the question: how certain are we about those ROIs?

Maybe Channel A’s ROI distribution is tightly clustered around £/€2.5, while Channel B’s is wide and skewed, with a long tail of possible outcomes.

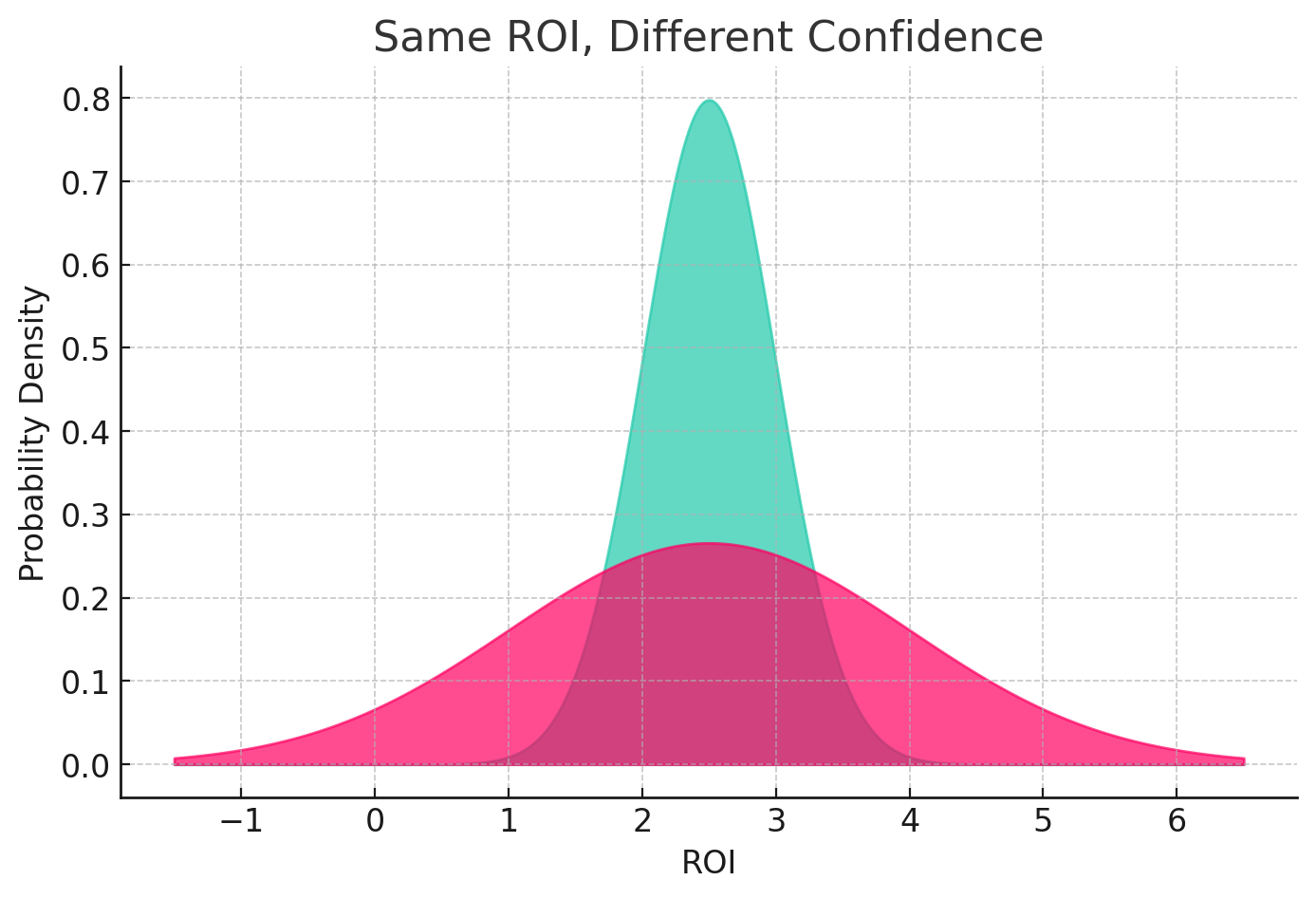
Does a varying outcome better reflect reality?

Now the decision shifts from a simple ranking exercise to a conversation about risk.

Would you rather invest in a predictable performer or one that might either greatly underperform or exceed expectations?

Distributions help you distinguish between “high potential” and “high confidence.” Both have value, but only one may suit your strategy today.

Simulating Optimisation Scenarios (bringing uncertainty to life with optimisation)

The powerful application of uncertainty is in optimisation. When running optimised scenarios using response curves, we simulate future outcomes and identify the media mix that maximises our returns.

But with distributions, we can simulate scenarios based on your desire for risk..

Want a conservative plan?

Use the 25th percentile of the response curves to simulate a downside scenario.

Keen to take more risks for a launch?

Use the 75th percentile. This is a practical way to turn uncertainty into planning flexibility.

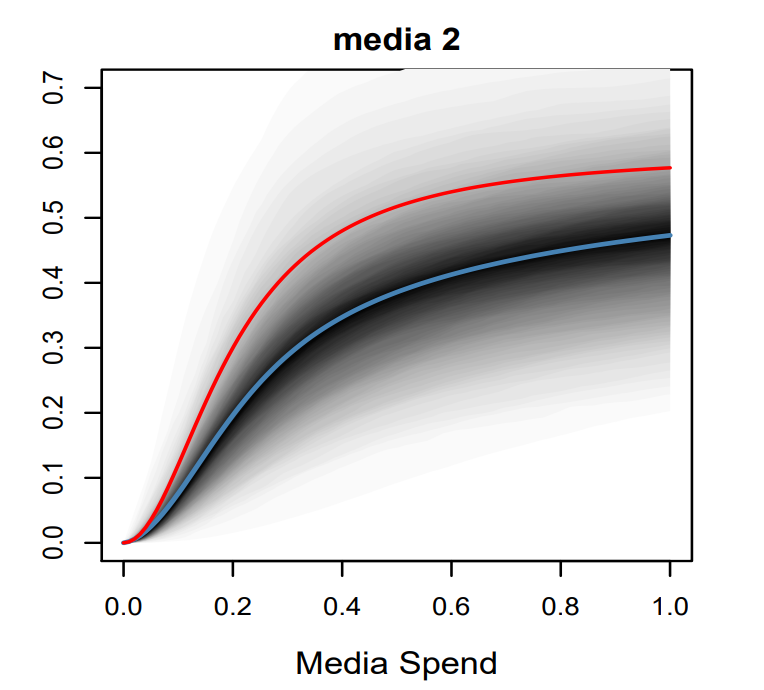
Instead of producing a single “optimal budget,” you now have a spectrum of scenarios. This makes your decisions more robust and allows for informed trade-offs between risk and return.

A Portfolio of Marketing Investments

In finance, portfolio theory doesn’t just look at the expected return of individual assets. It considers how those assets interact. The same logic applies to MMM.

When you have posterior distributions for each channel, you can also model how uncertainties across channels correlate.

Maybe two channels tend to underperform together, or maybe one picks up when another drops off. This covariance matters, especially when designing media plans that hedge against downside risk.

With Bayesian MMM, you can optimise for a portfolio of media channels and laydowns over time!

From Point Estimates to Smarter Decisions

Ultimately, modelling uncertainty isn’t about more complexity for its own sake. It’s about surfacing the range of what might happen and turning that into a competitive advantage.

Point estimates are simple and clean. But distributions help you plan, simulate, and optimise with greater confidence.

We run scenario’s not optimisations

At Linea, we seek to embrace the uncertainty of marketing. Our approach is focused on collaborating with brands to measure what's working with the aim of running multiple scenarios.

The best scenario? That’s dependent on your campaign objectives.

Leverage uncertainty to help you run more informed simulations for better planning and results.